俄国数学天才称平行线可以相交，遭嘲讽郁郁而

众所周知，两条平行线是绝对不可能相交的，而第五公设的存在使之成为可能。

正是这个第五公设让过去的许多数学家感到困惑，包括罗巴切夫斯基和他的父亲，他们一生都在试图证明第五公设。但遗憾结束。

为了延续父亲未完成的心愿，罗巴切夫斯基决定抛开一切，专心研究第五公设。

1815 年，罗巴切夫斯基着手研究第五条公理——这条尚未被欧几里德证明的公理，没有人怀疑这一假设。

多年来，过去的数学家们都竭尽全力证明这个假设，但都以失败告终。罗巴切夫斯基决定采取与其他人相反的方法。当所有人都证明了它的存在时，他就想方设法证明这个假设是站不住脚的。

罗巴切夫斯基花了几年时间才找到“矛盾的方法”。根据他的逻辑理论，在对第五公设反复提出否定命题后，一个新的公理体系诞生了。

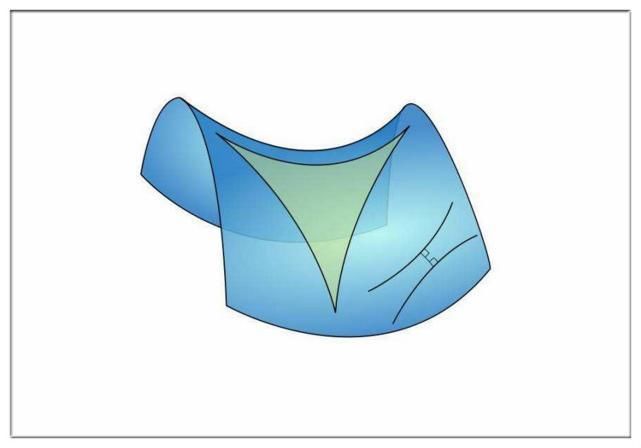然而，当时的学术界并不热衷于打破原有的结构，对这种畸形的理论提出质疑相继。 1826年，罗巴切夫斯基发表了一篇论文，这也是非欧几何的开端。

违反罗巴切夫斯基论文中描述的规则的命题与欧几里得的几何学非常不同。演讲结束后，在场的所有人都保持沉默，这也说明他们并不认同这个理论。

1829 年，罗巴切夫斯基重写了《几何原理》。 1832年，他请求被送交权威审查，但再次遭到嘲笑。

就这样，罗巴切夫斯基在一个一直受到质疑的社会中幸存下来。他的身体状况不如从前，而且他生病了。它非常沉重，最终失明了。 1856 年 2 月 12 日，罗巴切夫斯基遗憾地去世了。死的时候，他还在思考自己的论证论证，即使是瞎子，也没有放弃证明这个理论。

在他去世前一年，他向学生们口授并编写了《论几何》。让他对酒泉微笑的是，他的理论在12年后得到了证实，得到了学术界和世界的认可。

经过30年非欧几何的努力，罗巴切夫斯基的理论终于在1868年Bertrami发表的一篇论文中得到证实。Bertrami发表了一篇关于非欧几何解释的学术论文，基本是说非欧几何可以存在于欧几里得空间的表面上，注解了非欧几何的真实性。所有人都认为很荒谬的非欧几何，终于翻身了。

说到这里，肯定有人要问了，既然平行线的定义已经很清楚了，同一平面内不相交的两条直线叫做平行线。然后我们要讨论两条线的所谓双曲平面，以及它们在其他情况下是否相交。是否有意义？定义中所写的内容是不相交的。如果你最终证明它相交，那么它就不再属于平行线的定义了。你想称它们为平行线吗？

说到这里，首先，平行定理的前身是平行公理（parallel axiom），它源自欧几里得第五公理。它是数学大师欧几里得在他的《几何元素》一书中提出的五个公式中的第五个。这个独特的公理比前四个公理更复杂。前四个被证明是正确的。这第五条公理是平行定理的前身：另一位数学家将这条平行公理简化为：通过这条直线外的任何一点，只有一条直线与之平行。他的观点是大家普遍认可的。

在平面内不相交的两条直线称为平行线。事实上，它并不是科学界对平行线的严格定义，它只是一种流行的说法。

正是因为罗巴切夫斯基在这篇文章中对平行公设提出了一个反例，大家才发现第五公设有问题，重新定义了平行线的定义，加上了“在同一平面上”。这个限制。

这是第五个假设。两条我们不懂的平行线肯定会相交！事实证明，在我们对单个平面的理解中，两条平行线的不相交是正确的！

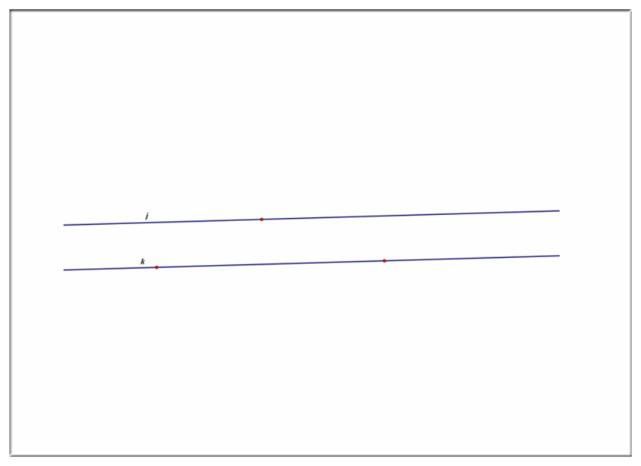欧几里德几何和非欧几何

老实说，非欧几何是真的很难被世界所接受。即使现在也一样。我一直认为波粒二象性实验与电子跃迁现象有关。但我不是专业人士，所以只能想象。我经常想知道过渡现象的存在是否证明了两个空间位置不同的平面实际上是一个平面，也就是说，空间中的任何一点在另一个平面上都有一个对应的点相互影响。这可能是量子现象的根本原因。

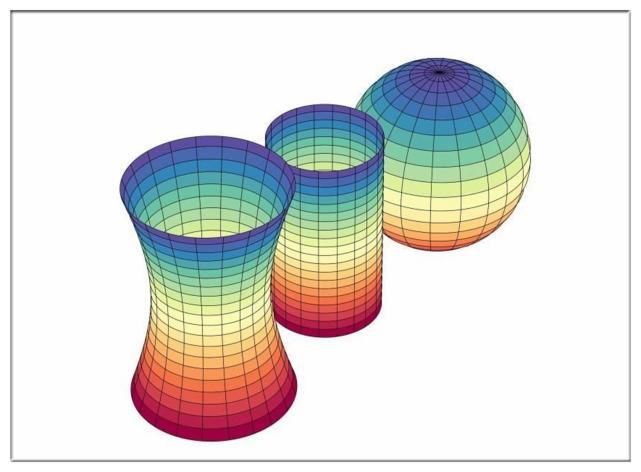
直观上讲，欧几里得几何就是平面上的几何，平面上的两条直线不会相交。 .在球面几何中，两条直线类似于地球上的经纬线，任何两条平行直线必定相交。我们说平面几何中两条直线在无穷远处相交。这也是一个模糊的概念。如果只是一个普通的平面，直线不会相交，即使它们很远。将无穷远处的点∞ 添加到平面时，平面会发生变化，从而使方形平面变成橘皮状。由于我们要求任何一条直线向外延伸时都达到无穷大点，无穷大就是所有直线的交点。

上一篇：如何处理模糊不确定的海量信息？
下一篇：没有了